终·搜索
前言
这应该是我讲搜索的最后一版课件了,里面大概有三个课件的内容,一次讲不完也很正常。(
这一版拥有几乎全部的搜索内容(不一定),所以你能见到的大部分搜索都可以用这里的知识解决(大概)。
(由于博客不支持目录所以没有目录了)
正文
搜索简介
搜索是一种神奇的算法,它在大部分题目中不是正解,但是却能在大部分情况下拿到分,有时很高,有时很低,但总归是有分。(
搜索分类
基本:dfs,bfs。
进阶:dfs 剪枝,bfs 优化,A*,迭代加深优化。
私货:DLX。
一.基础
DFS
简介
以深度为基本遍历顺序的搜索方式,其搜索顺序是树形的。
节点上的数字便是 dfs 的遍历顺序。
所以说我们认为 dfs 这个东西实现是十分简单的,它使用了递归的操作,分为两(三)部分,递归边界(剪枝)和递归转移,它最大的不同就是递归时有更多的选择(bushi)。
例 1 数字三角形
给定一个包含数字的n阶三角形,要求找到一条从三角形顶到底的一条路径,使得路径上所有数的和最大,并输出这个最大值。
样例输入:
1 | 5 |
样例输出:
1 | 30 |
也许你曾经见过这道题,而且你可能想用递推(或者说 dp)做这道题,但递推的本质其实是能找到合理规律的递归,所以如果数据范围小的话完全是可以过的。
例 2 八皇后问题
(不知道你们讲没讲过总之之前课件上有就扒下来了。
给定一个 8*8 的国际象棋棋盘,求在此棋盘上不重叠地放置八个皇后的方案。
要求:
皇后之间不能互相吃。
单个皇后的攻击范围为它的八个方向的直线。(上、下、左、右、左上、左下、右上、右下)
搜索最关键的地方就是判断转移是否成立,所以我们一定要把能否放置皇后的标志(flag)建立出来。
对于一个地方是否可以放置皇后,只需要判断在该行、该列以及斜对角上上是否有皇后即可。
针对行:记录数组 $a_i$判断第i行是否已放置了皇后。(可以省略)
针对列:记录数组 $b_i$ 判断第i列是否已放置了皇后。
针对左斜对角线:记录数组 $c_i$ 判断第 $i+j$ 个左斜对角线是否已有棋子。
针对右斜对角线:记录数组 $d_i$ 判断第 $i-j+7$ 个右斜对角线是否已有棋子。
(最后会有更快乐的算法高效解决这个问题。)
一些简单的好题
P1460 [USACO2.1]健康的荷斯坦奶牛 Healthy Holsteins
P1596 [USACO10OCT]Lake Counting S
BFS
以层次为基本遍历顺序的搜索方法,其搜索顺序显而易见是按层数来的。

树,但是是 bfs 序。
bfs 是要通过队列实现的,每次遍历到的点都进入到队尾,然后每次从队首找到一个点进行遍历(有的不是这样,是魔改的 bfs)。
例 1 求细胞数量
一矩形阵列由数字 0 到 9 组成,数字 1 到 9 代表细胞,细胞的定义为沿细胞数字上下左右若还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。
样例输入
1 | 4 10 |
样例输出
1 | 4 |
其实这个东西有一个更为规范的叫法——联通块。
根据题意,联通块有四联通,八连通..等等,我们直接一个简单的 bfs 敲上去,这题就出来了。
例 2 洛谷P2730 [USACO3.2]魔板 Magic Squares
一张有8个大小相同的格子的魔板:
1 2 3 4
8 7 6 5
这里提供三种基本操作,分别用大写字母“A”,“B”,“C”来表示(可以通过这些操作改变魔板的状态):
“A”:交换上下两行;“B”:将最右边的一列插入最左边;“C”:魔板中央四格作顺时针旋转。
下面是对基本状态进行操作的示范:
A: 8 7 6 5
1 2 3 4
B: 4 1 2 3
5 8 7 6
C: 1 7 2 4
8 6 3 5
对于每种可能的状态,这三种基本操作都可以使用。
你要编程计算用最少的基本操作完成基本状态到目标状态的转换,输出基本操作序列。
样例输入
1 | 2 6 8 4 5 7 3 1 |
样例输出
1 | 7 |
bfs有判重需要,如果我们采用不经过变化的 hash,将这个序列存在 $9*10^7$ 的数组里,程序就会炸掉,所以这道题还需要引入一个神奇的东西——康托展开。(stl_map:?)
使用康托展开可以将一个任意进制的数转换为十进制的数,在这道题中,我们用康托展开可以把数组空间节省至 8!=40320,是一个很大的优化。
好题
二.进阶
DFS 剪枝
你发现一些带着搜索tag的似乎用搜索做会TLE?
发现别人搜索的得分高说他不讲武德?
我说他们是瞎打的,朋友们啊,他们可不是瞎打,他们用了剪枝。
剪枝,顾名思义,我们会对我们的搜索树做一些不可描述的事情。
看见那些没用的状态了吗?
咔嚓一剪刀,树就被阉割了,他的负担就更少了,就跑的快了。
那么问题来了,怎么剪枝呢?
其实剪枝这事还挺简单的
比如你看见这里有棵树——
树呢?(剪没了)
你的剪枝一定需要保证是正确的!!!
剪枝的分类:上下界(玄学)剪枝,可行性(玄学)剪枝,最优化(玄学)剪枝,其他(玄学)剪枝。
上下界剪枝
这个东西十分直观,我们不需要什么花里胡哨的东西就能够理解,比如说拆数,总不能把 4 拆成 5+(-1) 吧。
因此,我们标定搜索的上下界,防止不必要的搜索节产生。
例 P1025 数的划分
将整数 $n$ 分成 $k$ 份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:$n=7$,$k=3$,下面三种分法被认为是相同的。
$1,1,5$; $1,5,1$; $5,1,1$。
问有多少种不同的分法。
样例输入
1 | 7 3 |
样例输出
1 | 4 |
对于这题,我们可以标定搜索的上下界,因为要求产生的数列不能够重复,所以我们搜索的下界是不能小于之前选过的数的最大值的。
同时,如果选的数字过大可能导致后边无数可拆,所以我们还要使用上界来对这个条件进行规划
加上上下界的标定后这题用 dfs 跑着就十分简单了。
搜索顺序
依据题目规定搜索的顺序(从大到小,从小到大 or 玄学)。
可行性剪枝
考虑当前转移是否符合题意,不符合删去。
例 UVA529 Addition Chains
一个与 $n$ 有关的整数加成序列 $
1.$a_0=1$
2.$a_m=n$
3.$a_0<a_1<a_2<…<a_{m−1}<a_m$
4.对于每一个 $k(1≤k≤m)$ 都存在有两个整数 $i$ 和 $j$($0≤i,j≤k−1$,$i$ 和 $j$ 可以相等),使得$a_k=a_i+a_j$。
给定一些 $n$,寻找最短步数时得到的序列。(输出任意一个解即可)
根据题意,我们可以得知 $a_k$ 的产生方式为 $a_{k-1}$(因为 选择两个非 $a_{k-1}$ 会导致 $a_k$ 小于 $a_{k-1}$)和之前任意的一项。
因为题目要求的是最短的序列,所以我们就可以把数向大赶,这样才能更快的找到解。
同时我们要进行可行性剪枝,设想:$a^k$ 能够产生的最大 $a_m$ 为 $2^ka_k$。所以太小的不会考虑。
最优性剪枝
当前大于目前答案时直接跳出。
比如前边的课后题 P1460 当当前的维生素袋数大于等于已经搜到的答案可以直接跳出。
额外的题
BFS 优化
双向搜索
假设我们现在要找网格图两点间的距离,但是存在一些障碍,我们考虑使用 bfs。
这是以起点单点搜索的范围:
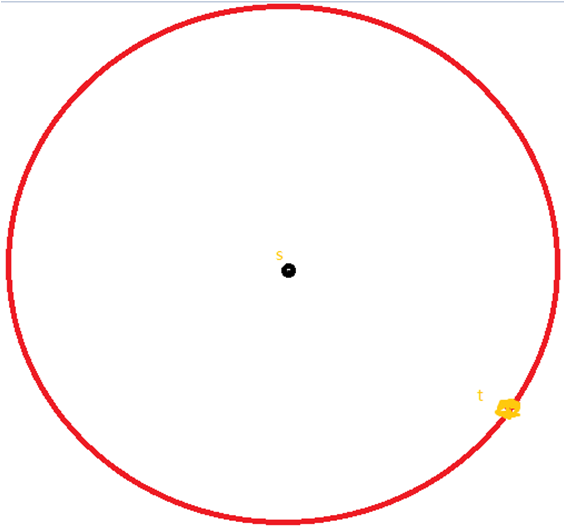
而这是以起点和终点两个起点搜索的范围:
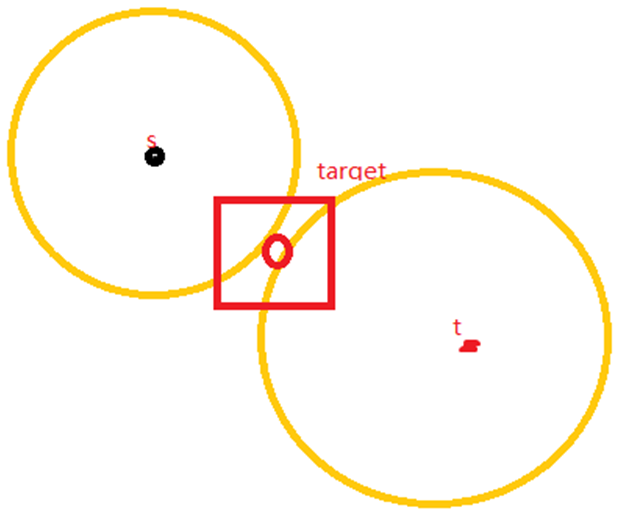
显然存在差距。
给出一种双向搜索的伪代码:
1 | while(!q1.empty()||!q2.empty()) |
修改队列
在某些情况下,使用一个裸的队列不能使算法正确,所以我们需要对队列进行一些修改。
例 电路维修
有一天某辆飞行车没有办法启动了,经过检查发现原来是电路板的故障。飞行车的电路板设计很奇葩,如下图所示:
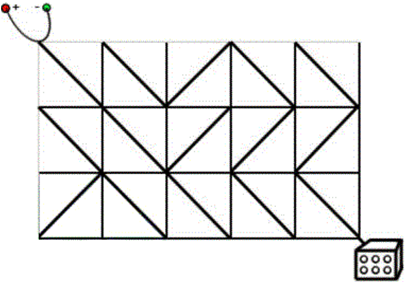
每次可以扭转一个电路板,使“/”与 “\”互换,求最少换几次使左上与右下联通。
解决方法:对于一个点,如果需要一次旋转才能到达目标点,就+1并插入队尾,如果不需要,就直接插入队首,防止 bfs 最优性出现问题。
如果翻转一个电路板要一个特定的价值呢?
把队列改成优先队列即可(也就是一个小根堆)。
这一部分内容无需特别练习,明白如何使用即可。
A*
引入
先来瞟一眼最短路问题。
仔细分析一下,堆优化的Dij其实就是一个优先队列的bfs。
但是这种策略有一个缺点,当前代价较小的的状态,接下来可能有很大的代价。这就导致了最优解可能出现的比较晚。
分析
我们很自然的想到一个对策,定义一个估价函数 $f(x)$,表示状态 $x$ 到最终状态的代价的咕计值,而每次扩展时依据的是“当前代价+咕值”最小的状态。并且,每个状态第一次出队,就是初始状态到它的最优解。
而这个估价函数 $f(x)$ 有一个很重要的性质,假设 $g(x)$为状态 $x$ 到最终状态的实际值,则:
$f(x)\leq g(x)$
我们尝试举个例子:

显而易见,最短路为最左边一条,代价为 17,但是由于这条边上的咕值过大导致结果出错(23),而如果保证 $f(x)]\leq g(x)$。
则即使某非最优解搜索路径上的状态 $s$,由于咕值不够准确,先被扩展了,但是:
由于 $s$ 并非最优,故随着当前代价不断累加,总有一时刻 $s$ 的当前代价大于从初始状态到目标状态的最小代价。
在最优解搜索路径上的状态 $t$,由于 $f(t)\leq g(t)$,故t的当前代价加上 $f(t)$ 小于等于从初始状态到目标状态的最小代价。
综上,$t$ 将被优先取出并扩展,并得到最优解。
而且我们想到,$f(x)$ 越接近 $g(x)$,越能更快得到最优解。
我们只需要把一个使用优先队列的 bfs 加上估价函数,就是 A*。
例 次短路
方法一:每次记录两个 dis 表示最短和次短,不再多说。
方法二:使用估价函数,其中估价函数 $f(x)$ 表示当前到终点的最短路,当终点第 $k$ 次从队中被取出时,就是 $k$ 短路。
A 板子 A 被卡了!请使用可并堆(另一种数据结构)通过魔法猪学园。
例 P1379 八数码难题
一个数如果想要恢复原位,必须至少移动曼哈顿距离次。(想一想,为什么)
所以估价函数直接设为一个状态到目标状态的曼哈顿距离之和。
判重随便搞就好,前边有康托,也可以使用 map 或者学习 hash。
迭代加深优化
ID 的全称:Adobe InDesign iterative deepening search
迭代加深可以从某种意义上减少搜索树的深度,提高程序效率。
IDDFS
在 DFS 的时候设置一个搜索层数限制,到了一个层数便返回,适合寻找那些奇妙的解。
我们设想一种极端的情况,对于一颗通常的搜索树来说,bfs 的转移十分难设计,而且占用空间,所以一般采用 dfs,但是某些图,dfs 效率十分低,因此我们可以将 IDDFS 视作 dfs+bfs,使 dfs 通过层数限制达到一定的目的。
实际上,限制的最大搜索层数的题都可以视为迭代加深。
例 P1189 ‘SEARCH’
这题如果用 dfs 实际上就要求了层数的限制,因此直接理解为迭代加深就可以了。
现在我们可以对三个基本的搜索(dfs,bfs,iddfs)进行一个比较了。
| 时间 | 空间 | 何时使用? | |
|---|---|---|---|
| DFS | $O(b^d)$ | $d$ | 图的规模不是十分离谱 |
| BFS | $O(b^d)$ | $b^d$ | 空间足够,规范的转移,期望最优答案 |
| IDDFS | $O(b^d)$ | $bd$ | 空间较小,接受效率的略微降低/限定步数 |
IDA*
A*+ID,懂?
实际上,A*是对 BFS 的优化。
IDA* 是对结合迭代加深的 DFS 的优化。
本质上是 bfs+dfs+f(x)。
例 P2324 骑士精神
iddfs 开搜,f(x):如果是白马设为一个值,如果是黑马设为另一个值,到时候判断是否与最终状态一致决定值就行了。
看到这里,你所有的搜索算法就掌握齐全了,还请各位多加练习,提升自己的搜索能力!
三.私货
八皇后的时候我曾提到一个其他算法可以解决这个问题,现在我们把它重拾起来。
八皇后看起来十分复杂,我们先换一个问题来解决。
例 矩阵覆盖问题
给定一个 $N$ 行 $M$ 列的矩阵,矩阵中每个元素要么是1,要么是0
你需要在矩阵中挑选出若干行,使得对于矩阵的每一列 $j$,在你挑选的这些行中,有且仅有一行的第 $j$个元素为 $1$。
首先,不可否认的是,我们可以用搜索解决这个问题,但是我们能否用另一种方式呢?
X 算法
X 算法